You are playing blackjack at the Turning Stone Casino. They are usinga single standard deck of 52 playing cards, and have already played outthe hands of all the players before you. The cards that you see on thetable are:
For example, if you find a blackjack table that pays 6 to 5 on a blackjack (a “natural”), run away. The house edge in that game, assuming all other rules are equal, is 0.4062% plus +1.3597% for a whopping 1.7659%. In a large casino, the house wins on its blackjack tables with a probability of 50.2%. All bets at blackjack are 1 to 1, which means that if you win, you gain the amount you bet, and if you lose, you lose the amount you bet.
J 9 A 5 7 8 10 2 K 6 6 ? 9
hand 1 hand 2 hand 3 you dealer
The dealer has one card turned down that you cannot see, denoted '?'.
The rules of blackjack are: all cards count their face value; J, Q,and K count as 10; aces A count as 1 or 11 at the players choice. You wantto draw cards and score as close as possible to 21 without going over.
a) It is your turn to draw or hold. If you draw a card, what is theprobability that you will go over 21?
b) What is the probability that you will end up with exactly 21?
Blackjack and Probability Chongwu Ruan Math 190S-Hubert Bray July 24, 2017 1 Introduction Blackjack is an usual game in gambling house and to beat the dealer and make money, people have done lots of research on it. They come up with several basic strategy which is consist of three tables corresponding to the different rules.
c) You actually draw a 6. How likely was that?
d) After you draw 6 in part (c), you have a total of 18. What is theprobability that the dealer already has a total greater than 18?
Solution:
a) We will go over 21 if we draw a card of value 10. There are 16 suchcards in a standard 52 card deck: 4 Ks, 4 Qs, 4 Js, 4 10s (henceforth wewill denote all these cards as '10's). Of the 13 cards on the table, thereare 3 cards that we know are 10s, plus the unknown card '?' of the dealerwhich might or might not be a 10.
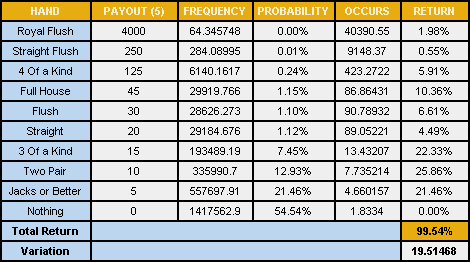
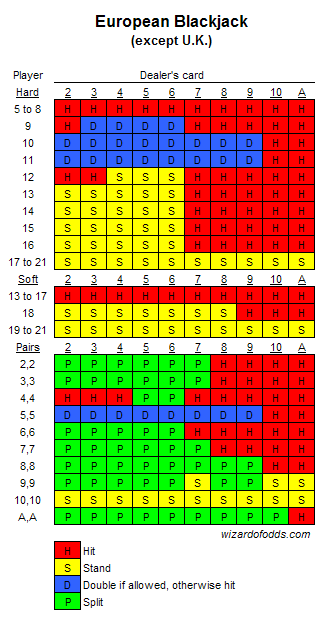
Blackjack Probability Tables
The probability we will draw a 10 depends on whether '?' is a 10 ornot. If '?' is a 10, then there are 4 10s on the table, and so 12 10s leftin the deck. Since the deck contains 39 remaining cards, we have:
prob to draw a 10 if '?' is a 10 = 12/39
If '?' is not a 10, then there are only 3 10s on the table, and so 1310s left in the deck. Since the deck has 39 cards remaining, we have:
prob to draw a 10 if '?' is not a 10 = 13/39
Now we need to figure out the probability that '?' is a 10 or not. Asidefrom '?' itself, there are 12 cards on the table, 3 of which are 10s. '?'clearly cannot be one of these 12 cards. It must be one of the 40 othercards, 13 of which are 10s. Hence:
prob '?' is a 10 = 13/40

The probability '?' is not a 10 is just 1-(13/40), since '?' eitheris or is not a 10, and so the probability for these two mutually exclusiveevents must sum to unity. Hence:
prob '?' is not a 10 = 27/40
Now we need to combine the above pieces to get our answer. We can divideup all outcomes in which we do draw a 10 into two mutually exclusive categories:(1) '?' is a 10, and (2) '?' is not a ten. The total probability is thereforethe sum of probabilities for the outcome to be in each category, i.e.
prob draw a 10 = (prob to draw a 10 if '?' is a 10) x (prob '?' is a10)
+ (prob to draw a 10 if '?' is not a 10) x (prob '?' is not a 10)
Note, now that we did the calculation the long way, we see that theanswer is the same was we would have gotten if we had completely ignoredthe card '?', i.e. assumed it was not on the table. In that case the probabilityto draw a 10 is just the 13 10s not face up on the table, divided by the40 cards not face up on the table. This works out correctly because, sincewe do not know anything about the value of '?', it plays a role identicalto any of the 39 cards remining in the deck. This way of thinking is abit subtle, so if you don't see it, the long way of doing the calculationas done above is the proof that it really is so.
b) For us to end up exactly with 21 we need to draw a 9. There are 49s in the deck, two of which are face up on the table. We can again dothe problem two ways. The long way as above is:
prob draw a 9 = (prob to draw a 9 if '?' is a 9) x (prob '?' is a 9)
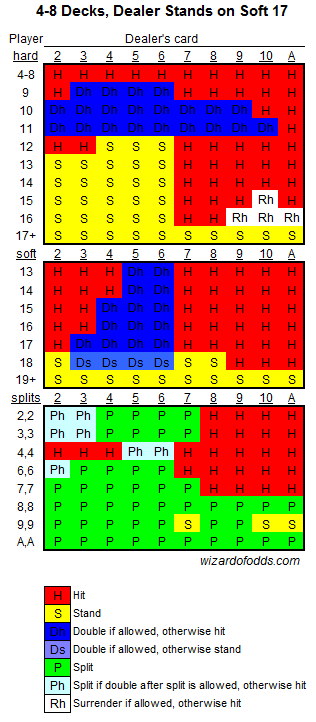
Blackjack Probability Tables Cheat
+ (prob to draw a 9 if '?' is not a 9) x (prob '?' is not a 9)
The short way is to ignore '?'. There are then 2 9s left in 40 cards,so the probability to draw a 9 is 2/40 = 0.05, the same answer as above.
c) There ar 4 6s in the deck, two of which are face up on the table.To get the probability we draw a 6, we can use the 'short' method. Thereare 2 6s left in 40 cards. The probability we drew a 6 is therefore
2/40 = 0.05
d) We have drawn a 6. There are now 13 cards face up on the table plus'?'. The probability that the dealer already has a total greater than 18is the probability that '?' has value 10, or is an Ace (which can countas 11 giving the dealer 20). There are 20 cards in the deck which are either10 or A. Four of these cards are face up on the table, so 16 remain inthe 39 cards that are not face up on the table. '?' is equally likely tobe any of these 39 cards. The probability the dealer already has greaterthan 18 is therefore:
16/39 = 0.41